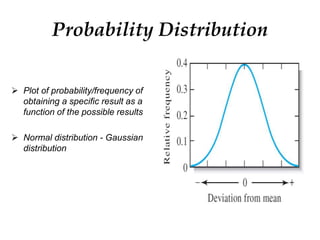
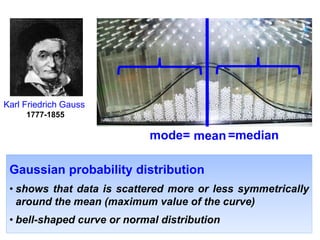
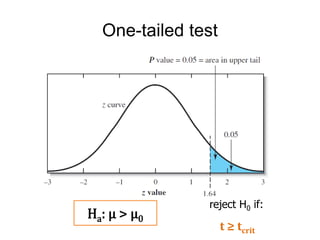
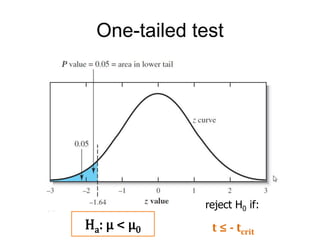
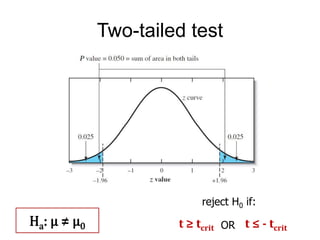
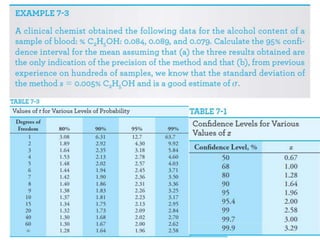
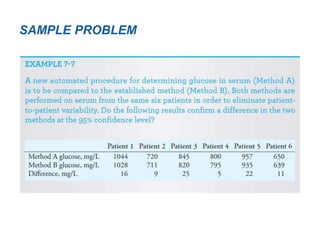
This document provides an outline and overview of key concepts related to experimental errors and statistics. It discusses significant figures in calculations, propagation of uncertainty, measures of central tendency and spread, characterizing experimental errors, and treating random errors with statistics. Specific topics covered include calculating uncertainties, confidence intervals, normal distributions, and distinguishing between random and systematic errors. The document uses examples and sample problems to illustrate key points about analyzing and interpreting experimental data.

2. Outline
Significant Figures in Numerical
Computations
Propagation of Uncertainty
Errors in Chemical Analysis
Measures of Central Tendencies
Measures of Spread
Characterizing Experimental Errors
Treating Random Errors with Statistics

3. RECALL
 Significant figures
- the minimum number of digits needed to write a given value in
scientific notation without loss of accuracy.
- Examples:
• 9.25 x 104
• 9.250 x 104
• 9.2500 x 104

4. Significant Figures in
Numerical Computations
“Determining the appropriate number of
significant figures in the result of an
arithmetic combination of two or more
numbers requires great care.”

5. Significant Figures in
Numerical Computations
 Sums and Differences
- the result should have the same number of decimal places as
the number with the smallest number of decimal places.
3.4 + 0.020 + 7.31 = 10.730 (round to 10.7)
= 10.7 (rounded)
 Products and Quotients
- answer should be rounded so that it contains the same number
of significant digits as the original number with the smallest
number of significant digits. Unfortunately, this procedure
sometimes leads to incorrect rounding.

6. Significant Figures in
Numerical Computations
 Logarithms and Antilogarithms
𝒏 = 𝟏𝟎 𝒂 𝑚𝑒𝑎𝑛𝑠 𝑡ℎ𝑎𝑡 𝐥𝐨𝐠 𝒏 = 𝒂
1. In a logarithm of a number, keep as many digits to the right of
the decimal point as there are significant figures in the original
number.
log 339 = 2.530 The number of SF in the mantissa should
equal the number of SF in the original
number.
characteristic mantissa

7. Significant Figures in
Numerical Computations
 Logarithms and Antilogarithms
𝒏 = 𝟏𝟎 𝒂 𝑚𝑒𝑎𝑛𝑠 𝑡ℎ𝑎𝑡 𝐥𝐨𝐠 𝒏 = 𝒂
2. In an antilogarithm of a number, keep as many digits as there
are digits to the right of the decimal point in the original
number.
antilog (-3.42) = 10-3.42 = 3.8 x 10-4 The number of SF in the antilogarithm
shoul equal the number of digits in the
mantissa.
2 digits 2 digits

8. Propagation of Uncertainty
 Absolute Uncertainty
- Expresses the margin of uncertainty associated with
a measurement.
- For example, if the buret on the right has an absolute
uncertainty of  0.02 mL and when the reading is
30.25 mL, the true value could be anywhere in the
range 30.23 to 30.27 mL

9. Propagation of Uncertainty
 Relative Uncertainty
- Compares the size of the absolute uncertainty with
the size of its associated measurement.
- The relative uncertainty of a buret reading of
30.25  0.02 mL is
𝑅𝑒𝑙𝑎𝑡𝑖𝑣𝑒 𝑈𝑛𝑐𝑒𝑟𝑡𝑎𝑖𝑛𝑡𝑦(𝑅𝑈) =
𝐴𝑏𝑠𝑜𝑙𝑢𝑡𝑒 𝑢𝑛𝑐𝑒𝑟𝑡𝑎𝑖𝑛𝑡𝑦
𝑚𝑎𝑔𝑛𝑖𝑡𝑢𝑑𝑒 𝑜𝑓 𝑚𝑒𝑎𝑠𝑢𝑟𝑒𝑚𝑒𝑛𝑡
𝑅𝑈 =
0.02 𝑚𝐿
30.25 𝑚𝐿
= 0.0007
%𝑅𝑈 = 100 𝑥 𝑅𝑈 = 0.0007 𝑥 100
= 0.07 %

10. Propagation of Uncertainty
 Addition and Subtraction
𝑒4 = 𝑒1
2
+ 𝑒2
2
+ 𝑒3
2
1.76 (0.03)
+ 1.89 (0.02)
– 0.59 (0.02)
Uncertainty in
addition and
subtraction
3.06 (0.04) (Absolute Uncertainty)
3.06 (1%) (Relative Uncertainty)
3.06
e1
e2
e3
(e4)
𝑒4 = 0.03 2 + 0.02 2 + 0.02 2 = 0.041
%𝑅𝑈 =
0.041
3.06
𝑥100 = 1.3 %

11. Propagation of Uncertainty
Uncertainty in
multiplication and
division
 Multiplication and Division
– First convert all uncertainties to percent relative
uncertainties. Then calculate the error of the product as
follows:
– Example:
%𝑒4 = %𝑒1
2 + %𝑒2
2 + %𝑒3
2
%𝑒4 = 0.02 2 + 0.01 2 + 0.03 2 = 0.039
1.76(0.03) + 1.89(0.02)
0.59(0.02)
= 5.64𝑒4
(Absolute Uncertainty)
5.64 (0.22)
(Relative Uncertainty)
5.64 (4%)
1.76(2%) + 1.89(1%)
0.59(3)
= 5.64𝑒4

12. 1. Calculate the molar concentration of 8.45 (0.473%) mL
0.2517 (1.82%) g/mL ammonia solution that was
diluted to 0.5000 (0.0002) L.
(Ans. 0.250 (0.005) M)
2. Consider the function pH= –log[H+], where [H+] is the
molarity of H+. For pH = 5.21  0.03, find [H+] and its
uncertainty.
(Ans. 6.2 (0.4) x 10-6)
SAMPLE PROBLEM

14. Errors in Chemical Analysis
 Difference between a measured value and
the "true" or "known" value
 Estimated uncertainty in a measurement or
experiment

15. Errors in Chemical Analysis
Replicates
– Samples of about the same size that are carried out
through an analysis in exactly the same way
– TRIALS - minimum of 2

16. Measures of Central Tendency
Mean
– most widely used measure of central value
– also called the arithmetic mean or the average.

17. Measures of Central Tendency
Median
- middle result when replicate date are
arranged in increasing or decreasing order
 For odd number of results, locate the middle
 For even number of results, average value of
middle pair
Mode
- value that has the highest frequency

18. Measures of Central Tendency
coin number mass of coin, g mass of coin, g
1 5.0305 5.0098
2 5.0383 5.0305
3 5.1118 5.0383
4 5.0827 5.0476
5 5.1123 5.0825
6 5.0098 5.0827
7 5.0476 5.1118
8 5.1118 5.1118
9 5.0825 5.1118
10 5.1118 5.1123

19. Measures of Spread
1. Range
- difference between the largest and smallest values in the data
set
2. Deviation
3. Average deviation
4. Standard deviation
– describes the spread of individual measurements about the
mean
5. Variance
– square of standard deviation
6. Relative Standard Deviation (RSD)
– can be expressed in terms of ppt or %
– coefficient of Variation (CV)

20. Measures of Spread

21. 1. For each set, calculate the mean, median, range,
standard deviation and coefficient variation.
SAMPLE PROBLEM
Set A 0.812 0.792 0.794 0.900
Set B 70.65 70.63 70.64 70.21

22. 2. Consider the following values
Calculate the mean, median, range, deviation, average
deviation, standard deviation, RSD and CV.
SAMPLE PROBLEM
821.0 783.0 834.0 855.0

23. 3. The following data were collected as part of a quality
control study for the analysis of sodium in serum;
results are concentrations of Na+ in mmol/L.
Report the mean, the median, the range, the standard
deviation, and the variance for this data.
SAMPLE PROBLEM
140 142 141 137 122
157 142 149 118 145

24. CHARACTERIZING
EXPERIMENTAL ERRORS
 Errors associated with the central tendency
reflect the accuracy of the analysis
 Errors associated with the spread reflect the
precision of the analysis

25. PRECISION
• Deviation
• Average deviation
• Standard deviation
• Variance
• Coefficient of variation
ACCURACY
• Absolute error
• Relative error
1 2
3 4

26. CHARACTERIZING
EXPERIMENTAL ERRORS
Accuracy
– Measure of how close a measure of central
tendency is to the true or expected value ()
– Expressed in terms of:
1. Absolute Error
2. Relative Error

27. CHARACTERIZING
EXPERIMENTAL ERRORS
Accuracy
1. Absolute Error
– difference between the measured value and the true value
– Sign: (-) measurement result is low
(+) measurement result is high
2. Relative Error
– More useful quantity than the absolute error

28. CHARACTERIZING
EXPERIMENTAL ERRORS
Precision
– Measure of spread of data about a central value
– Errors affecting the distribution of measurements
around a central value are called indeterminate and
are characterized by a random variation in both
magnitude and direction

29. CHARACTERIZING
EXPERIMENTAL ERRORS

30. Precision
1. Repeatability
 the precision for an analysis in which the only source of
variability is the analysis of the replicate sample
e.g. acid content ( two trials)
2. Reproducibility
 the precision when comparing results for several samples
for several analyst or for several methods
CHARACTERIZING
EXPERIMENTAL ERRORS

31. CHARACTERIZING
EXPERIMENTAL ERRORS
Errors affecting ACCURACY:
Determinate/Systematic Errors
 flaw in an experiment/design of an experiment
 can be discovered or corrected
 causes the mean of a data set to differ from the
accepted value
 e.g. loss of volatile analyte while heating the sample

32. CHARACTERIZING
EXPERIMENTAL ERRORS
Errors affecting PRECISION:
Indeterminate/Random Errors
 Causes the data to be scattered more or less
symmetrically around a mean value because they are
small enough to avoid individual detection
 Always present and cannot be corrected
 Minimize errors by increasing the number of
determinations (n)
e.g. electricity fluctuations, temperature, etc.
IDEAL:  error  average deviation (both precise and accurate)

33. RANDOM SYSTEMATIC
Affects ? Precision Accuracy
Are results
reproducible?
NO
has an equal chance
of being (+/-)
YES
since results are
usually constant in both
magnitude & direction
Can be
determined?
NO
always present
YES
Can be eliminated/
corrected?
NO
but can be minimized by
increasing the number
of trials
YES
Types of Errors in Experimental Data

34. CHARACTERIZING
EXPERIMENTAL ERRORS
Gross Errors
 differ from indeterminate and determinate errors
 occur only occasionally, often large and may cause
results to either high or low.
 often the product of human errors
 e.g. precipitate is lost before weighing, touching a
weighing bottle with your fingers
 results to outliers!!!

35. GROSS
Affects ? Accuracy
Are results
reproducible?
NO
has an equal chance
of being (+/-)
Can be
determined?
YES
Can be
eliminated/
corrected?
YES
Leads to?
Outliers
results that appear to
differ significantly from
the rest of the data
Types of Errors in Experimental Data

36. 1. Instrumental errors
 non-ideal instrument behavior
 faulty calibrations
 inappropriate conditions*
2. Method errors
 non-ideal chemical or physical behavior
of analytical systems
3. Measurement errors
 due to limitations in the equipment and
instruments used to make
measurements e.g. analytical balance
Sources of Systematic Errors

37. 4. Sampling errors
 When sampling strategy fails to provide
a representative sample e.g. soil
sampling (heterogeneous sample)
5. Personal errors
 carelessness, inattention
 personal limitations of the experimenter
Sources of Systematic Errors

38. TREATING RANDOM ERRORS WITH
STATISTICS
Population
Collection of all measurements
of interest to the experimenter.
Sample
Subset of measurements
selected from the population.

39. Population
Entire blood supply!!!
Sample
Small amounts of blood
Determination of glucose in the blood of a diabetic patient

40. Probability Distribution
 Plot of probability/frequency of
obtaining a specific result as a
function of the possible results
 Normal distribution - Gaussian
distribution

41. Karl Friedrich Gauss
1777-1855
Gaussian probability distribution
• shows that data is scattered more or less symmetrically
around the mean (maximum value of the curve)
• bell-shaped curve or normal distribution
meanmode= =median

42. Parameter
A quantity that defines a
population.
Statistic
An estimate of a parameter
made from a sample of data.42

43. PARAMETER STATISTIC
Population mean µ Sample mean
Population standard deviation σ Sample standard deviation s
Properties of a Gaussian Curve
N – total number of measurements*

46. At 90% confidence level,
the lead content of
gasoline
lies within 2.5 ± 0.3 ppm.
1. Confidence interval
2. Confidence limits
3. Confidence level
4. Significance level
Range of values within which
the true mean is expected to
lie with a certain probability.
Boundaries of the confidence
interval.
Probability that the true mean
lies within the certain interval.
Probability that the result is
outside the confidence
interval.

47. Confidence Interval for Populations
𝑋𝑖 =  ± 𝑧𝜎

48. Confidence Interval for Populations
SAMPLE PROBLEM
What is the 95% confidence
interval for the amount of aspirin in
a single analgesic tablet drawn
from a population where  is 250
mg and 2 is 25?
SOLUTION
𝑋𝑖 =  ± 1.96𝜎 = 250 𝑚𝑔 ± 10 𝑚𝑔
Thus, we expect that 95% of the
tablets in the population contain
between 240 and 260 mg aspirin.

49. Confidence Interval for Populations
Alternatively, a confidence interval
can be expressed in terms of the
population’s standard deviation
and the value of a single member
drawn from the population.
𝜇 = 𝑋𝑖 ± 𝑧𝜎

50. Confidence Interval for Populations
SAMPLE PROBLEM
The population standard deviation
for the amount of aspirin in a batch
of analgesic tablets is known to be
7 mg of aspirin. A single tablet is
randomly selected, analyzed, and
found to contain 245 mg of aspirin.
What is the 95% confidence
interval for the population mean?
SOLUTION
𝜇 = 𝑋𝑖 ± 𝑧𝜎 = 245 ± 1.96 7
= 245 ± 14 mg
There is, therefore, a 95 % probability
that the population’s mean, , lies
within the range of 231-259 mg of
aspirin.

51. Confidence Interval for Populations
Confidence interval can also be
reported using the mean for a
sample of size n, drawn from a
population of known . The CI for
the population’s mean, therefore, is

52. Confidence Interval for Populations
SAMPLE PROBLEM
What is the 95% CI for the
analgesic tablets described in the
previous example, if an analysis of
five tablets yield a mean of 245 mg
of aspirin?
SOLUTION
𝜇 = 245 ±
(196)(7)
5
= 245 𝑚𝑔 ± 6 mg
Thus, there is a 95% probability that
the population’s mean is between 239
and 251 mg of aspirin.

53. Confidence Interval for Populations
Confidence interval can also be
reported using the mean for a
sample of size n, drawn from a
population of known . The CI for
the population’s mean, therefore, is

54. For N ≥ 20, DF = N
For N < 20, DF = N-1
For N-1 degrees of freedom, s is said to be an unbiased
estimator of σ

55. Finding the Confidence Interval
CASE: when σ is unknown
for N measurements:
Student’s t

56. critical values

57. One-tailed test
Ha: µ > µ0
reject H0 if:
t ≥ tcrit

58. One-tailed test
Ha: µ < µ0
reject H0 if:
t ≤ - tcrit

59. Two-tailed test
Ha: µ ≠ µ0
reject H0 if:
t ≥ tcrit t ≤ - tcritOR

62. SIGNIFICANCE TESTING
Designed to determine whether the difference
between two values is too large to be explained by
indeterminate errors.

63. Statistical Aids to Hypothesis Testing
Null Hypothesis
H0
Assumes that the numerical
quantities being compared
are the same.

64. Alternative Hypothesis
Ha
Difference between values is
too great to be explained by
random error.
Statistical Aids to Hypothesis Testing

65. Determining whether the
concentration of lead in an
industrial wastewater discharge
exceeds the maximum permissible
amount of 0.05 ppm.
H0: µ = 0.05 ppm µ > 0.05 ppm
Experiments over a several year
period have determined that the
mean lead level is 0.02 ppm.
Ha:
µ = 0.02 ppm µ ≠ 0.02 ppmHa:H0:

66. ERRORS IN SIGNIFICANCE
TESTING
Type 1 error
The risk of falsely rejecting the
null hypothesis ()
Type 2 error
The risk of falsely retaining the
null hypothesis ()

67. STATISTICAL METHODS FOR
NORMAL DISTRIBUTIONS
A. Comparing an experimental mean with a
known value
B. Comparing two sample means
C. Comparing two standard deviations (F-test)
D. Dixon’s Q-test (Test for outliers)

68. To carry out the statistical test, a test procedure must be
implemented. The crucial elements of a test procedure are:
1. formation of an appropriate test statistic &
2. identification of a rejection region.
The test statistic is formulated from the data on which we will base the
decision to accept or reject H0. The rejection region consists of all the
values of the test statistic for which H0 will be rejected.
A. COMPARING AN EXPERIMENTAL
MEAN WITH A KNOWN VALUE

69. Large Sample z Test
If a large number of results are available so that s is a good estimate of s,
the z test is appropriate. The procedure that is used is summarized below:
A. COMPARING AN EXPERIMENTAL
MEAN WITH A KNOWN VALUE

70. Small Sample t Test
For a small number of results, we use a similar procedure to the z test
except that the test statistic is the t statistic.
A. COMPARING AN EXPERIMENTAL
MEAN WITH A KNOWN VALUE

72. • e.g. two sets of data from the same analysis performed
by two different analysts
• Requires that the standard deviations of the two data
sets being compared are EQUAL
H0: µ1 = µ2 Ha: µ1 ≠ µ2
Ha: µ1 > µ2
Ha: µ1 < µ2
two-tailed test
one-tailed test
B. COMPARING TWO SAMPLE MEANS
The t Test for Differences in Means

73. • DF = N1 + N2 - 2
• test statistic:
Reject H0 if: t > tcrit
t < - tcrit
B. COMPARING TWO SAMPLE MEANS
The t Test for Differences in Means

74. 𝑠 𝑝𝑜𝑜𝑙𝑒𝑑 =
𝑠 𝐴
2
𝑁𝐴 − 1 + 𝑠 𝐵
2
(𝑁 𝐵 − 1)
𝑁𝐴 + 𝑁 𝐵 − 2
Alternatively,

75. SAMPLE PROBLEM
In a forensic investigation, a glass containing red wine
and an open bottle were analyzed for their alcohol content
in order to determine whether the wine in the glass came
from the bottle. On the basis of six analyses, the average
content of the wine from the glass was established to be
12.61% ethanol. Four analyses of the wine from the bottle
gave a mean of 12.53% alcohol. The 10 analyses yielded a
pooled standard deviation spooled = 0.070%. Do the data
indicate a difference between the wines at the 95%
confidence level?

76. • same type of procedure as the normal t test except that we
analyze pairs of data and compute the differences, di
H0: µd = 0
Ha: µd ≠ 0
Ha: µd > 0
Ha: µd < 0
two-tailed test
one-tailed test
B. COMPARING TWO SAMPLE MEANS
Paired Data

77. • Test statistic
𝑡 =
đ − 0
𝑠 𝑑
𝑁
B. COMPARING TWO SAMPLE MEANS
Paired Data

78. SAMPLE PROBLEM

79. • The critical value of t is 2.57 for the 95% confidence level and 5 degrees of
freedom.
• Since t > tcrit , we reject the null hypothesis and conclude that the two
methods give different results.

80. • DF1 = N1 - 1
• DF2 = N2 - 1
One-tailed test H0: σ1 = σ2
Ha: σ1 > σ2 or
σ1 < σ2
Two-tailed test H0: σ1 = σ2
Ha: σ1 ≠ σ2
C. COMPARING TWO STANDARD DEVIATIONS
(F-test)
F-test: tells us whether two standard
deviations are significantly different from
each other

81. Test statistic: F = s1
2/s2
2 for s1 > s2
Reject H0 if: F > Fcrit
C. COMPARING TWO STANDARD DEVIATIONS
(F-test)

82. A standard method for the determination of the CO level in gaseous
mixtures is known from many hundreds of measurements to have a
standard deviation of 0.21 ppm CO.
A modification of the method yields a value for s of 0.15 ppm CO for a
pooled data set with 12 degrees of freedom. A second modification,
also based on 12 degrees of freedom, has a standard deviation of 0.12
ppm CO.
1. Determine whether the precision of the second modification is
significantly better than that of the first.
2. Is either modification significantly more precise than the original?
SAMPLE PROBLEM

83. SAMPLE PROBLEM
𝐹 =
𝑠1
2
𝑠2
2 =
(0.15)2
(0.12)2
= 1.56
𝐻 𝑜: 𝑠1
2
= 𝑠2
2
𝐻 𝑎: 𝑠1
2
≠ 𝑠2
2
In this case, Ftab = 2.69. Since F < 2.69, we must accept Ho and
conclude that the two methods give equivalent precision.
𝐻 𝑜:  𝑠𝑡𝑑
2
= 1
2
𝐻 𝑎:  𝑠𝑡𝑑
2
> 1
2
𝐹1 =
𝑠𝑠𝑡𝑑
2
𝑠1
2 =
(0.21)2
(0.15)2
= 1.96
𝐹2 =
𝑠𝑠𝑡𝑑
2
𝑠2
2 =
(0.21)2
(0.12)2
= 3.06
Ftab = 2.30
Since F1(1.96) < 2.30, we must
accept Ho and conclude that there is
no improvement in the precision.
Since F2(3.06) > 2.30, we must reject
Ho and conclude that it appears that
the second modification give better
precision.

84. xq = questionable result
xn = neighboring result
w = range
Q > Qcrit : Reject questionable value
Q < Qcrit : Retain questionable value
D. DIXON’S Q-TEST(Test for Outliers)
NOTE: Data should be ordered.
Outlier – a data point that differs excessively from the mean in a data set

85. xq = questionable result
xn = neighboring result
w = range
D. DIXON’S Q-TEST(Test for Outliers)

86. SAMPLE PROBLEM
The analysis of a city drinking water for arsenic yielded
values of 5.60. 5.64, 5.70, 5.69, and 5.81 ppm. The last
value appears anomalous; should it be rejected at the 95%
confidence level?
𝑄 𝑐𝑎𝑙𝑐 =
5.81 − 5.70
5.81 − 5.60
= 0.52
Since Qcalc(0.52) < Qtab(0.710), retain
the value. 5.81 ppm is NOT an
outlier.

87. References
Skoog, D. A., West, D. M., Holler, F. J., & Crouch, S. R. (2014). Skoog and
Wests Fundamentals of Analytical Chemistry.
Harris, D.C. (1999). Quantitative Chemical Analysis.
Harvey, D. (2000). Modern Analytical Chemistry.