Ejemplos de ejercicios resueltos de estadística
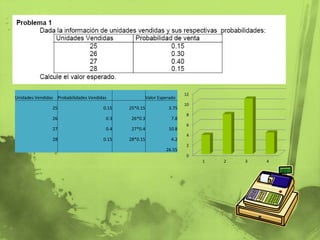
- 1. 0 2 4 6 8 10 12 1 2 3 4 Unidades Vendidas Probabilidades Vendidas Valor Esperado 25 0.15 25*0.15 3.75 26 0.3 26*0.3 7.8 27 0.4 27*0.4 10.8 28 0.15 28*0.15 4.2 26.55
- 2. Juego Premio P.E. Valor Esperado Ganar 50,000 0.550000*0.5 25000 Perder 50,000 0.550000*0.5 25000 50000 0 5000 10000 15000 20000 25000 1 2
- 3. Cantidad Tipo de premio Valor del premio Probabilidad Valor esperado 1 mayor 1000 0.000000667 0 1000*0.000000667 0.000667 2 secos 50 0.000000667 0 50*0.000000667 0.00003335 2 secos 20 0.000000667 0 20*0.000000667 0.00001334 100 secos 2 0.000000667 0 2*0.000000667 0.000001334 149 Secos 0.5 0.000099333 0 0.5*0.000099333 0.000049666 0.00076469 0 0.0001 0.0002 0.0003 0.0004 0.0005 0.0006 0.0007 1 2 3 4 5
- 5. Alternativa S1 Probabilidad S2 Probabilidad S3 Probabilidad Valor Esperado A1 $50 0.30 $70 0.50 $100 0.20 70 A2 $90 0.30 $40 0.50 $80 0.20 63 A3 $70 0.30 $60 0.50 $90 0.20 69 202 58 60 62 64 66 68 70 1 2 3
- 7. P=0.0001 N=20000 Binomial with n = 20000 and p = 0.0001 x P( X <= x ) 2 0.676676 = 0.323324
- 8. A) Binomial with n = 20 and p = 0.2 x P( X <= x ) 2 0.206085 B) Binomial with n = 20 and p = 0.2 x P( X = x ) 4 0.218199 C) Binomial with n = 20 and p = 0.2 x P( X <= x ) 3 0.411449
- 9. A) Binomial with n = 12 and p = 0.1 x P( X = x ) 2 0.230128 B) Binomial with n = 12 and p = 0.1x P( X <= x ) 1 0.659002 C) Binomial with n = 20 and p = 0.1x P( X <= x ) 0 0.121577
- 10. A) Binomial with n = 2 and p = 0.03 x P( X = x ) 0 0.9409 B) Binomial with n = 2 and p = 0.03 x P( X = x ) 1 0.0582 C) Binomial with n = 2 and p = 0.03 x P( X = x ) 2 0.0009
- 12. media=5 P(x<3)=p(0)+p(1)+p(2) Cumulative Distribution Function Poisson with mean = 5 x P( X <= x ) 2 0.124652
- 13. media=5 P(x>10)=1-[ p(0)+p(1)+p(2)+…+p(10)] Cumulative Distribution Function Poisson with mean = 5 x P( X <= x ) 10 0.986305 1 – 0.986305 = .013695
- 14. p=.001 n= 3000 a) media= np =(.001)(3)=.003 b) P(x=0) Probability Density Function Poisson with mean = 3 x P( X = x ) 0 0.0497871
- 15. Media=2000 ℓ=200 P(2000≤ x ≤ 2400) Cumulative Distribution Function Normal with mean = 2000 and standard deviation = 200 x P( X <= x ) 2000 0.5 Cumulative Distribution Function Normal with mean = 2000 and standard deviation = 200 x P( X <= x ) 2400 0.977250 0.977250 – 0.5 = 0.47725
- 16. Media=13 cm σ=0.1 P(13≤ x ≤ 13.2) Cumulative Distribution Function Normal with mean = 13 and standard deviation = 0.1 x P( X <= x ) 13 0.5 Cumulative Distribution Function Normal with mean = 13 and standard deviation = 0.1 x P( X <= x ) 13.2 0.977250 0.977250 – 0.5 = 0.47725
- 17. Media=980 ℓ=48 a) P(x≥1000) b)P(x≤940) c)P(960 ≤ x ≤ 1060) a) Cumulative Distribution Function Normal with mean = 980 and standard deviation = 40 x P( X <= x ) 1000 0.691462 1-0.691462=0.308538 b) Cumulative Distribution Function Normal with mean = 980 and standard deviation = 40 x P( X <= x ) 940 0.158655 c) Cumulative Distribution Function Normal with mean = 980 and standard deviation = 40 x P( X <= x ) 960 0.308538 Cumulative Distribution Function Normal with mean = 980 and standard deviation = 40 x P( X <= x ) 1060 0.977250 0.977250 – 0.308538= 0.668712
- 18. Media=5.10 ℓ=0.40 a) P(x≥5.4) b)P(4.70 ≤ x ≤5.4) c)P(x ≥3.40) a) Cumulative Distribution Function Normal with mean = 5.1 and standard deviation = 0.4 x P( X <= x ) 5.4 0.773373 b) Cumulative Distribution Function Normal with mean = 5.1 and standard deviation = 0.4 x P( X <= x ) 4.7 0.158655 0.773373 - 0.158655 =0.614718 c) Cumulative Distribution Function Normal with mean = 5.1 and standard deviation = 0.4 x P( X <= x ) 3.9 0.0013499 1 – 0.0013499 = 0.9987
- 19. N=1500 n=300 p=300/1500 = 0.2 q=1-0.2= 0.8 Nievl de Confianza= 0.99 α= 1 -0.99 = .01 z= -2.5758293 0.22660305* 1500= 339.904576LS 0.17339695* 1500= 260.095424LI a) b) 0.21032796*1500= 315.491933LS 0.18967204*1500= 284.508067LI Cota del error [284.50, 315.49]
- 20. N1=100 N2=100 Media=1425 Media=1905 σ=40 σ=30 Cota del error 2.83666003 1.16333997
- 21. N=2500 n=85 p=0.65 q=1-0.65=0.35 Nievl de Confianza= 0.97 Nivel de Confianza= 0.85 α= 1 -0.97 = 0.03 α= 1 -0.97 = 0.15 z= -2.17009038 z= -1.43953147 0.67070134* 85= 57.0096141LS 0.663732255*85= 56.4172417LS 0.62327468* 85= 52.9783479LI 0.632271735*85= 53.7430975LI
- 22. M=5.3 σ=1.2 n=26 5.783327959 LS Nievl de Confianza= 96% 4.816672041 LI α=0.04 z= -2.05374891 Verdadera Media= 5
- 24. H0= m1=m2 HA: m1≠m2 One-Sample T Test of mu = 55 vs not = 55 N Mean StDev SE Mean 99% CI T P 17 50.00 7.00 1.70 (45.04, 54.96) -2.95 0.010 Inverse Cumulative Distribution Function Student's t distribution with 16 DF P( X <= x ) x 0.01 -2.58349 Rechazamos H0 por que la T calculada es > que la de tablas Afirmamos con el 99% de probabilidades que no es posible que la media de la población sea 55.
- 25. H0= m1 = m2 H4: m1≠m2 G1= n1+n2-2 =8+14-2=20 Two-Sample T-Test and CI Sample N Mean StDev SE Mean 1 8 50.00 5.00 1.8 2 14 45.00 4.00 1.1 Difference = mu (1) - mu (2) Estimate for difference: 5.00 95% CI for difference: (0.50, 9.50) T-Test of difference = 0 (vs not =): T-Value = 2.42 P-Value = 0.032 DF = 12 Inverse Cumulative Distribution Function Student's t distribution with 20 DF P( X <= x ) x 0.05 -1.72472 T> que la t de tabla, se rechaza Ho Por lo tanto si existe una diferencia significativa entre las medias
- 26. t= (σ₁²-σ₂²) √n-2 1.60416667 2σ₁σ₂√1-r₁₂² Inverse Cumulative Distribution Function Student's t distribution with 49 DF P( X <= x ) x 0.01 -2.40489 Se acepta H0 por que la t de tablas es mayor que la calculada
- 27. Two-Sample T-Test and CI: Campaña 1, Campaña 2 Two-sample T for Campaña 1 vs Campaña 2 N Mean StDev SE Mean Campaña 1 6 20.17 5.98 2.4 Campaña 2 6 22.17 7.25 3.0 Difference = mu (Campaña 1) - mu (Campaña 2) Estimate for difference: -2.00 99% CI for difference: (-14.47, 10.47) T-Test of difference = 0 (vs not =): T-Value = -0.52 P-Value = 0.615 DF = 9 Inverse Cumulative Distribution Function Student's t distribution with 10 DF P( X <= x ) x 0.01 -2.76377 H0: m1≠m2 H1: m1≠m2 Aceptamos Ho
- 28. Inverse Cumulative Distribution Function Student's t distribution with 18 DF P( X <= x ) x 0.05 -1.73406 √1 - r² 0.189 n-2 0.6±1.73(.189)= 0.6±0.3 = [.91, .23] La variabilidad del coeficiente esta entre 0.91 y 0.27
- 29. H0; r1=r2 Hq; r1≠r2 n= 50 r1= 0.72 -0.24 -0.520307601 r2= 0.78 0.611751584 r= 0.6 -0.850521053 Inverse Cumulative Distribution Function Student's t distribution with 47 DF P( X <= x ) x 0.05 -1.67793 t T calculada es < t de tablas; por tanto aceptamos H0
